Arrimo Capacitação pedagógica

Aprenda

Como estudar

Como estudar Matemática?

Dez mandamentos para professores

Os 11 conselhos de Bill Gates

Como fazer uma boa leitura

Livros para gostar de Matemática

DICAS

Formulário de Matemática

Formulário de Física

Site construído por Francisco Ismael Reis           E-mail: fireis@arrimo.com.br

(11) 4324-0555   •  (11) 99626-8935

No ar desde: 06/01/2011

Fonte: http://www.matematica.pt/util/formulas.php

.

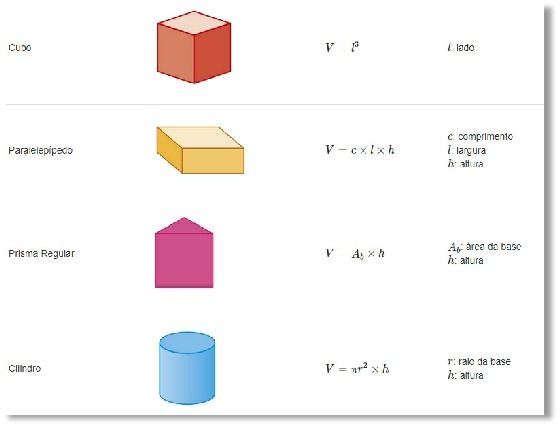
Clique na imagem para visualizar o formulário completo.

Formulário de Matemática